Platte, Scheibe, Fläche, Decke, Wand

Thema: Bemessungsschnittgrößen für Flächentragwerke

Allgemeines

Für die Bemessung von Flächentragwerken (außer Platten) stehen zwei Verfahren für die Ermittlung der Bemessungsschnittgrößen zur Verfügung. Im Folgenden werden die Berechnungsgrundlagen vorgestellt und Hinweise zur Anwendung gegeben.

Vorzeichenkonvention: Zugkräfte und -spannungen erhalten ein positives Vorzeichen. Alle Beziehungen gelten für in Bewehrungsrichtung transformierte Schnittgrößen.

DIN EN V 1992-1-1:1991

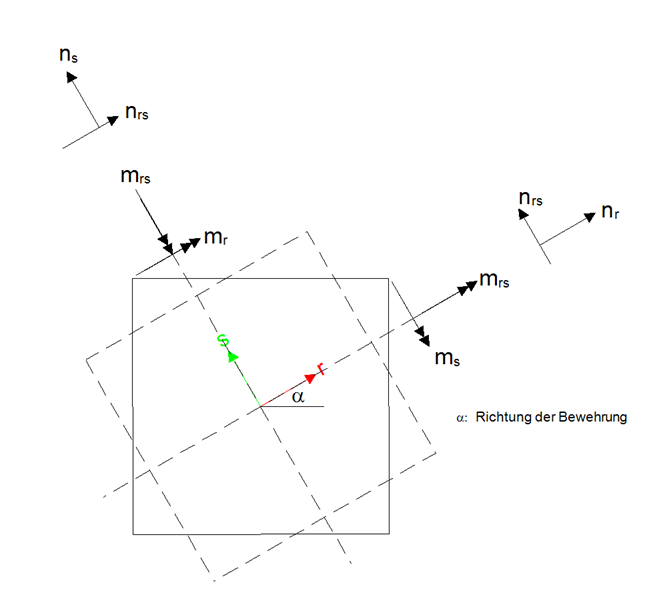
Das Verfahren zur Ermittlung der Bemessungsschnittgrößen für Flächentragwerke in MicroFe orientiert sich an dem Algorithmus, welcher im Anhang 2 des Eurocode 2, Teil 1-1, (Deutsche Fassung ENV 1992-1-1: 1991), Juni 1992, beschrieben ist.

Anhang A2.8 - Bewehrung in Platten

- Rechtwinkliges Koordinatensystem

- Die Richtungen x und y werden so gewählt, dass m_y ≥ m_x

m_r ≥ m_s: m_y = m_r; m_x = m_s

m_r < m_s: m_y = m_s; m_x = m_r

- Ermittlung der Bemessungsmomente gemäß Flussdiagramm

- m_udx und m_udy bewirken Zug an der Plattenunterseite

- m'_udx und m'_udy bewirken Zug an der Plattenoberseite

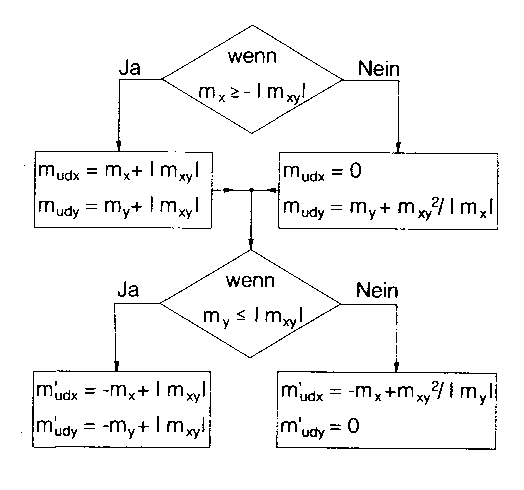
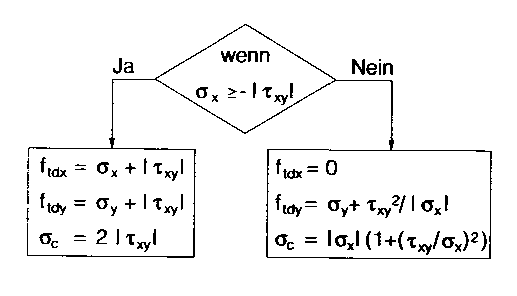
Anhang A2.9 - Bewehrung in Scheiben und Wänden

- Rechtwinkliges Koordinatensystem

- Die Richtungen x und y werden so gewählt, dass σ_y ≥ σ_x

- f_tdx und f_tdy angenommene rechnerische Zugspannungen,
für die der Beton in x- und y-Richtung zu bewehren ist

- Wird die Zugfestigkeit des Betons vernachlässigt, ergeben sich die
Bewehrungsgrade in x- und y-Richtung zu ρ_x=f_tdx/f_yd und ρ_y=f_tdy/f_yd,
wobei negative Werte zu Null gesetzt werden sollten.

- Zusätzlich werden die Betondruckspannungen begrenzt
σ_c ≤ σ_Rd = ν * f_cd

Druckknoten: v = 1,0 * η₁

Druck-Zugknoten:

nach DIN EN 1992-1-1/NA, NDP zu 6.2.3(3) bzw. NDP zu 11.6.2(1)
v = v₁ = 0,75 * η₁ * v₂
mit
v₂ = (1,1 - f_ck / 500) ≤ 1,0
η₁ = 1,0 (Normalbeton)
η₁ = 0,40 +0,60 * ρ / 2200 (Leichtbeton)
mit
ρ: Trockenrohdichte in (kg/ m³)

Werden die Bedingungen nach A2.9(3) nicht eingehalten, so erfolgt keine Bemessung, sondern für den entsprechenden Knoten wird eine Druckspannungsüberschreitung ausgewiesen. Als Bemessungsnormalkraft n_Ed wird dann -MAX( σ_c, 2 * | τ_xy |) * Flächendicke ausgegeben.

Schalen (kombinierte Beanspruchung aus Biegung, Normal- und Querkraft)

Die Bemessungsmomente werden entsprechend dem Flussdiagramm für die Plattenbeanspruchung ermittelt.

Die Normalkräfte werden aus Spannungen gemäß Flussdiagramm für die Scheibenbemessung integriert.

n_Ed = σ_c * h
h: Plattenstärke

σ_c: Betondruckspannung gemäß Flussdiagramm für Scheiben

Hinweise

Das Verfahren berücksichtigt keine günstig wirkenden Drucknormalspannungen. Das heißt bei kombinierter Beanspruchung aus Biegung und Druck bleibt die Zugbewehrung bei wachsender Normalspannung konstant.

Option: Membran-Druckbewehrung

Die Option steht nur bei dem Berechnungsverfahren nach DIN EN 1992-1-1:1991 zur Verfügung.

Die Option dient der Bewehrungsermittlung im Bereich von Betondruckspannungsüberschreitungen.

Ermittlung der Hauptspannung und der Hautrichtung α
Bemessung in Richtung der zweiten Hautspannung σ₂
Umrechnung der ermittelten Druckbewehrung in Bewehrungsrichtung
a_sx = cos² (α) * a_sr + sin² (α) * a_ss
a_sy = sin² (α) * a_sr + cos² (α) * a_ss

Thürlimann

Die Ermittlung der Bemessungsschnittgrößen erfolgt in Anlehnung an den statischen Grenzwertsatz der Plastizitätstheorie [1].

Bemessungsschnittgrößen

m_{r,
bem} = m_r ± |m_rs|
m_{s,
bem} = m_s ± |m_rs|
n_{r,
bem} = n_r ± |n_rs|
n_{s,
bem} = n_s ± |n_rs|
n_c = -2 * |n_rs|
m_c = ± 2 * |m_rs|

Aus den Schnittgrößenkombinationen (m_r, n_r) und (m_s, n_s) werden diejenigen Kombinationen gesucht, die die maximale Zugbewehrung liefern.

Zusätzlich werden die Betondruckspannungen begrenzt

σ_c (n_c; m_c) ≤ σ_Rd = ν * f_cd

Druckknoten: v = 1,0 * η₁

Druck-Zugknoten:

Hinweise

Das Verfahren berücksichtigt günstig wirkende Drucknormalspannungen, das heißt bei einer kombinierten Beanspruchung aus Biegung und Druck reduziert sich die erforderliche Zugbewehrung mit wachsender Drucknormalspannung.

[1] Thürlimann B., Marti P., Pralong J., Ritz P., Zimmerli: "Anwendung der Plastizitätstheorie auf Stahlbeton", Institut für Baustatik und Konstruktion, ETH Zürich, 1983

mb WorkSuite 2018 \| MicroFe - Hilfe
.